直齿轮考研盘点，看完你全懂了！

发布日期：2022-12-12 点击：

齿轮作为机械原理中花费篇幅最长、内容最多的机构，学习起来并不是一件特别容易的事，这篇文章会列举齿轮中基础的内容——直齿轮的相关重要知识点。

齿廓啮合基本定律：一对齿轮的传动比等于其连心线被接触点公法线所分割的两线段的反比。

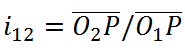
图片9.png

也就是说，两齿轮的传动比取决于O₁、O_2、P 三点的位置，又因为O₁、O₂与机架固结是固定不动的，因此传动比仅由P点在连心线上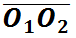的位置决定。其中P点被称为节点，以两轮的轴心为圆心，过节点在两个齿轮上各做一个圆，称为齿轮的节圆，节圆半径分别为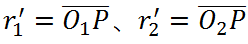图片11.png 。其中α' 为节圆压力角。

图片1.png

现实生活中的齿轮传动，不一定都是定传动比，P点是可能在连心线上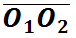图片12.png 随时间变化而变动的，传动比可能不恒定，只有当P点固定在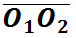某个位置上时，才是定传动，那怎样的齿轮才能满足这个条件呢，接下来就要引出我们今天的主角——渐开线齿轮。

那什么是渐开线呢？

渐开线

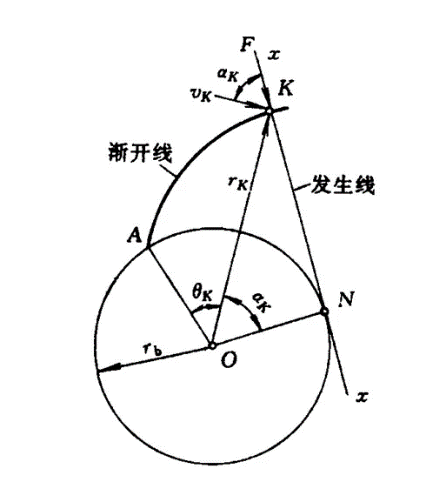
图片2.png

渐开线的形成过程是：是一直线NK沿一固定圆周做纯滚动，此时直线上任一点K的轨迹就是渐开线，有渐开线齿廓的齿轮就被称作渐开线齿轮。该固定圆被称为渐开线的基圆。
图片3.png 基于渐开线的形成过程，其作为齿廓时的特性如下：

渐开线特性：

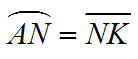
(1) 图片13.png
(2) 渐开线上任一点的法线都与基圆相切
(3) 渐开线的形状取决于基圆大小。基圆半径越大，渐开线的曲率半径越大。
(4) 基圆内无渐开线。

渐开线齿廓啮合特点：

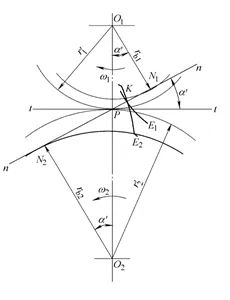
(1)齿廓间正压力方向始终沿着接触点公法线方向保持不变。根据渐开线的性质可知，过两齿轮接触点K的公法线必定与两齿轮的基圆相切，而传动过程中基圆的大小和位置都保持不变，因而齿廓间正压力方向保持不变。

(2)定传动比：由（1）可知，公法线是一条固定的直线，那么与连心线的交点P为一个固定点，由齿廓啮合基本定律可知，渐开线齿廓能保持定传动比。

(3)传动比可分性：下图中△O₁N₁P与△O₂N₂P相似，可得：

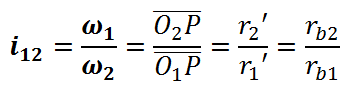
图片14.png

由于已确定的渐开线齿廓的基圆是不变的，以此即使两齿轮安装中心距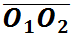图片12.png 略有偏差，也不会影响两齿轮的传动比。

渐开线齿轮相关计算

上述概念基本上是选择题或判断题的常客，大家一定要记住。接下来就是相关计算的问题了，为了节省篇幅我们这里先给出渐开线标准直齿轮的相关几何尺寸的计算公式。

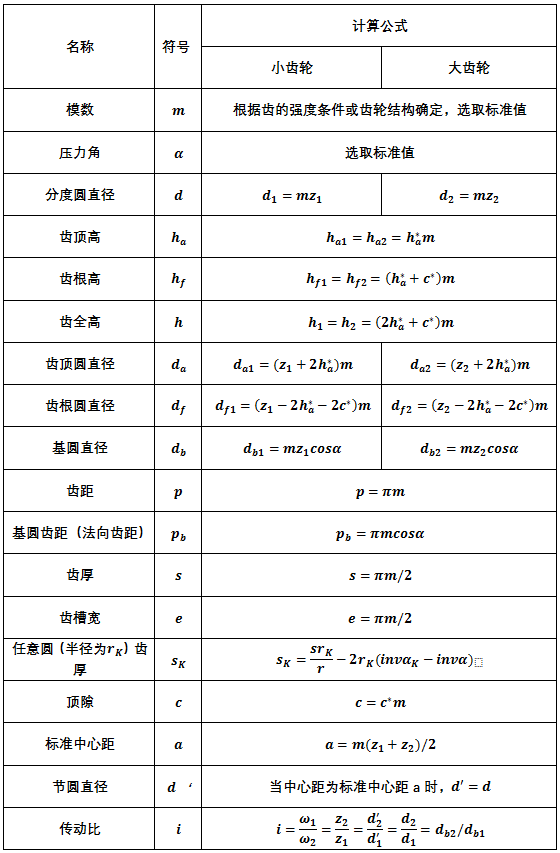
图片15.png

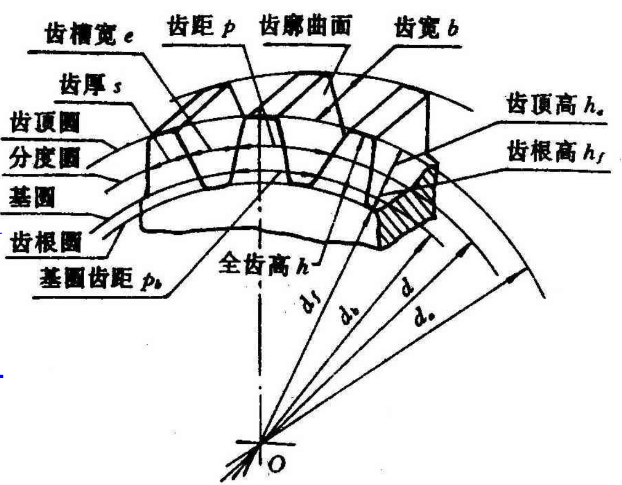
图片4.png

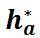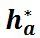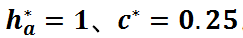如果大家有在本科阶段学习过机械原理的话，这些尺寸肯定不陌生，一般题目我们选取的都是标准齿轮，标准齿轮的定义如下：把m、α、、c^*取为标准值，齿厚等于齿槽宽的齿轮称为标准齿轮。对于正常齿制的齿轮，图片16.png 、c*取标准值图片18.png 。

考题中都会先给你模数的值，再进行后面的计算，没有的话也会告诉你某些条件让你能够计算出齿轮的模数，比如告诉你齿轮的中心距和齿轮的齿数Z₂，Z₂通过方程

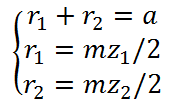
图片19.png

可以轻松得到模数的大小
其中模数m虽然是人为选取的，但它最开始是由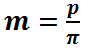图片20.png 得到的，之后被我们标准化作为齿轮自身的一个参数，在设计时直接选取就好了。不仅模数被标准化了，分度圆压力角也被标准化了，那大家知道我们为什么要这样做吗？

原因是不同的模数和分度圆压力角，就对应着不同形状的齿轮，那么加工时就需要由不同的刀具来加工，如果说不进行标准化对模数和分度圆压力角的待选取数量进行限制的话，理论上可以有无数种刀具来进行各个不同的齿轮加工，这样庞大的数量对齿轮的加工成本和使用都是不利的，因此要对齿轮的模数和分度圆压力角进行标准化。

渐开线齿轮正确啮合条件

经过上述的介绍我们已经可以很熟练的计算渐开线齿轮的各个参数了，但在我们的使用过程中发现，并不是任一对渐开线齿轮都能正确啮合进行传动，只有当两齿轮的法向齿距KK'相等时，才能进行正确啮合传动，而由渐开线特性(1)可知它与基圆齿距p_b是相等的，即p_b₁₌p_b₂，由基圆齿距的计算公式

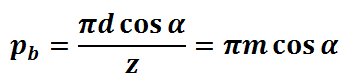
图片21.png

可得:

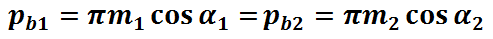
图片22.png

由于模数和分度圆压力角均已标准化，所以m₁=m₂=m，α₁=α₂=α，这样就得到一对渐开线齿轮正确啮合条件为：两轮的模数相等，两轮的压力角相等。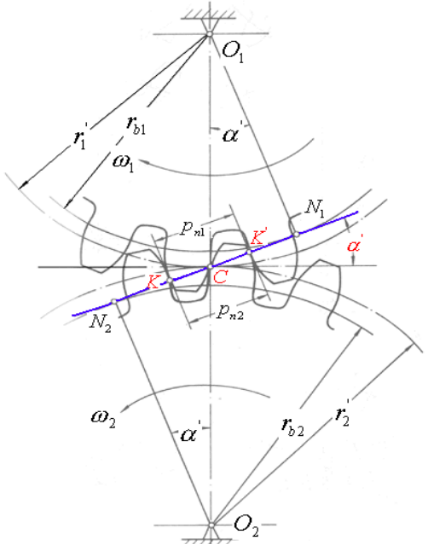
图片5.png

渐开线齿轮连续传动条件

在解决了渐开线齿轮正确传动的问题后，我们就要考虑如何才能保证在传动过程中的平稳连续。接下来我们先了解一下当渐开线齿轮可以连续传动时的情况。

当两渐开线齿轮的一对轮齿进入啮合时，主动轮的齿根部分与从动轮齿顶接触于B2点，脱离啮合时，从动轮的齿根部分与主动轮的齿顶接触于B1点。称B1为啮合终止点，在图上表现为主动轮齿顶圆和从动轮齿根圆的交点，B2为啮合起始点，在图上表现为主动轮齿根圆和从动轮齿顶圆的交点。线段B1B2为实际啮合线段。其中轮齿啮合的公法线与两齿轮的切点N₁和N₂被称为啮合极限点，连接成的线段为理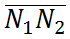图片23.png 论啮合线。

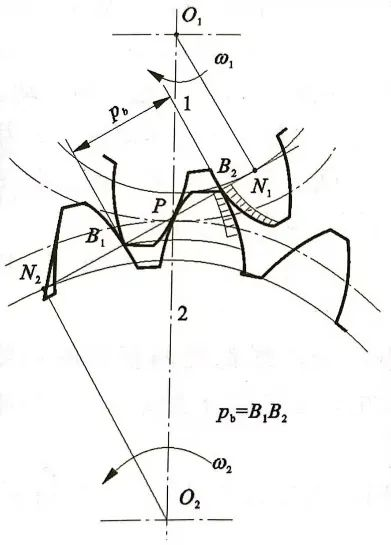
图片6.png

为了使两齿轮能连续传动，就需要满足实际啮合线要大于齿轮的法向齿距。这里就要引入一个重合度ε的概念，它的计算公式为: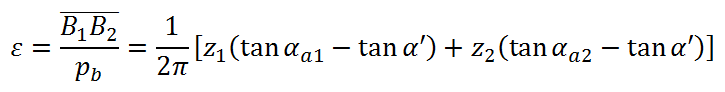

当ε≥1时即能满足齿轮连续传动的条件。注意这里公式中的α'为啮合角的大小，即齿轮啮合点处速度方向和受力方向的夹角，也被称为节圆压力角。由于在标准安装时，齿轮的节圆与分度圆相等，故分度圆压力角等于啮合角α'=α，若为非标准安装时，啮合角的大小需要用如下公式计算，rcosα=r'cosα'，事实上，该公式计算的是基圆半径r_b的大小，类似的还有r_b=r_acosα_a=r_fcosα_f。

根切现象

要理解根切现象，需要先理解齿轮的加工方法。齿轮的加工方法主要有仿形法和范成法（展成法），由于仿形法效率低、精度差，所以目前用得较多的是范成法。

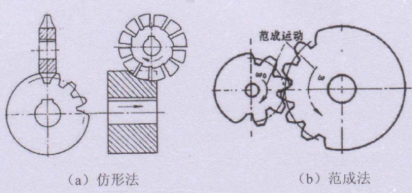
图片7.png

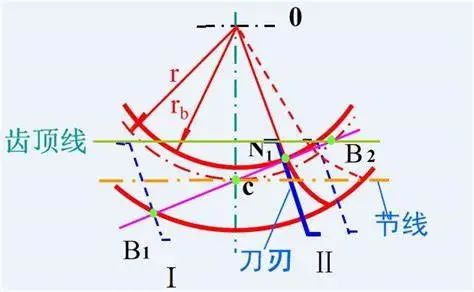
范成法的原理就是运用齿廓啮合的基本定律，用具有渐开线齿廓的刀具包络切制除被切齿轮的渐开线齿廓。用以切制的刀具常常选择齿条插刀或滚刀（除此之外，还有齿轮滚刀、剃形刀等），相较于标准齿条，齿条形刀具的齿顶高要高出c^*m的距离，用以是齿轮齿根处留出顶隙。加工时使刀具分度线和待切齿轮分度圆相切并做纯滚动，就能加工出标准齿轮的齿廓。由于是做纯滚动，则齿轮分度圆半径和齿条速度满足ν=ωr，又因r=1/2mz所以被加工齿数与齿条刀具加工时的速度的关系为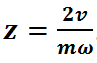图片25.png 。由此，我们可以知道，同一种齿条刀具加工出来的齿轮模数、压力角都是一样的，不同的只可能因加工时齿条刀具速度不同而加工出不同齿数，即不同大小的齿轮。根切现象就是在此加工过程中，刀具顶部过多地切入了轮齿根部，因而将齿根的渐开线齿廓切去了一部分。根切现象会导致轮齿抗弯强度降低，对传动不利，重合的也会降低。那是什么原因导致即使在加工过程中刀具的分度线与被加工齿轮的分度线重合也会出现根切现象呢，简单来说就是被加工齿轮的齿数过少，导致齿轮过小，其极限啮合点低于了齿条刀具的齿顶线，对于标准齿轮来说，不产生根切现象的最少齿数是17。